Have you ever been curious about what algorithm is behind Array.sort()? After all, we've learnt so many sort algorithms, each has their advantages and disadvantages.

Chrome's engine v8 turned out to be using a non-classic sort algorithm - Tim Sort. It was created in 2002 by one of the Python major contributor Tim Peters for improving the Python list sort performance. The combination of the algorithms it uses was decided by analysing the real world data. In comparison of Quick Sort, which in the worst case executes O(n2) time, the worst case of it is just O(nlog n). And its best could achieve O(n). Here is a table of the famous sorting algorithms, and their complexities, stabilities:

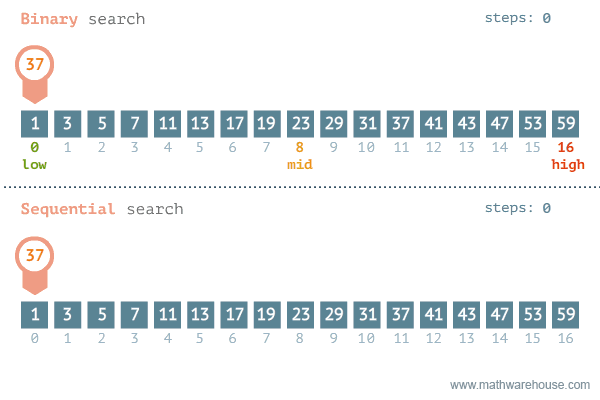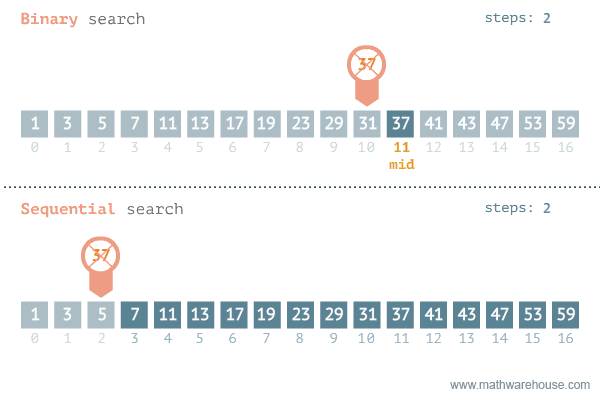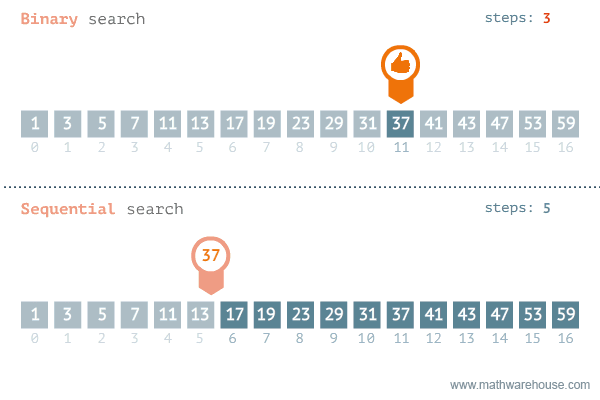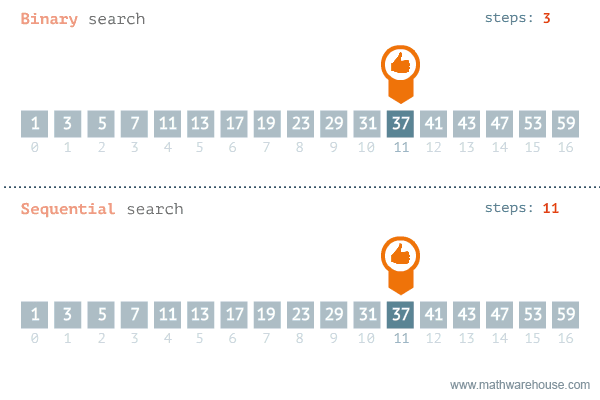
To reduce the operations, it's more common to use the "upgraded version" of Insertion Sort - Binary Sort, which combines Binary Search to speed up the progress of looking for the right place for each item.

Enable to keep the stability and achieve the best performance. Tim decided to use Insertion Sort when the list length is small.

Insertion sort is a classic sorting algorithm that basically do a forward comparison one-by-one to find the item smaller than or equals to it, and move it to the place after this smaller item (assume we are sorting in ascending order). Here is a straight forward GIF:

To reduce the operations, it's more common to use the "upgraded version" of Insertion Sort - Binary Sort, which combines Binary Search to speed up the progress of looking for the right place for each item.

When it comes to a long list, Tim sort will use the idea of Merge Sort - divides the long list into smaller "runs" and conquer one-by-one, then merge them together back.

Here's a straight forward GIF:

Divide to runs

When using the classic Merge Sort, we often simply divide list to runs in a fixed size - like 2. Tim experimented and compared different run sizes, and found slightly larger run size will perform better, which is around 32~64 inclusive. You may ask why 32 and 64? Where was these numbers come from? This was because the Python performance measuring tool Tim used could only test powers of 2 sizes data.

In the meantime, he also found in the real world data, there are many parts of data sorted either in ascending or descending order, which do not require sorting. Thus, he decided to divide runs in a "natural" size - the size of initial runs are not in a fixed number, but have a minimal size requirement - "min run".

Here is how it divides:

1. Set a descending flag by comparing the first 2 items, if there is only 1 item left, then set as false.
2. Loop the following items, and check if they are still in ascending or "strict" descending order, util finding the item which does not follow this order.
3. Now we have a run in either ascending or "strict" descending order. If it is in "strict" decending order, do reverse it. Only do reserse on the "strict" descending part to keep the sorting stable.
4. Then we check whether this run length satisfies my "min run" constraint. If it is smaller than my "min run" constraint, compensate the following items to make it achieve the min size. And do a binary sort starting from the compensated items, avoiding sort the sorted items again.